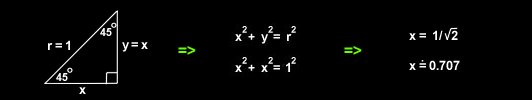Special Trigonometry Ratios for 30o,60o,45o Angles - Math Teaching Help - Game Tips:
- A 60 degree angle is special since it is found in every equilateral triangle.
Splitting an equilateral triangle in half, yields two right triangles, each having 30, 60 & 90 degrees.
- For each 30,60,90 right triangle, the sides have special ratios. Begin with hypotenuse length = 1 unit.
The side opposite the 30o angle is half the length of the side opposite the 90o angle
and the side opposite the 60o angle can be found from x2 + y2 = r2 , namely (1/2)2 + y2 = (1)2 .
So each 30,60,90 right triangle has sides in the special ratio 0.5 / 0.866 / 1.0 approx.

- Basic Trigonometry uses the ratios of the 'lengths of sides' of triangles as related to 'angle size'.
- A 45 degree angle is also special since it is found twice in every right isosceles triangle.
- For each 45,45,90 right triangle, the sides have special ratios. Use hypotenuse r=1.
A side opposite one 45o angle can be found from x2 + y2 = r2 , namely x2 + x2 = (1)2 .
So each 45,45,90 right triangle has sides in the special ratio 0.707 / 0.707 / 1.0 approx.
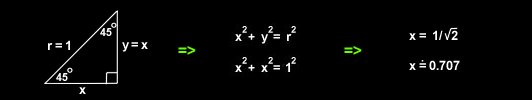
- When angle DAE is in standard position at a graph's origin (0,0) then sin A equals (y/r),
cos A equals (x/r),
and tan A = (y/x).
- When r=1 then the primary Trig ratios simplify to sin A = y,
cos A = x,
and tan A = (y/x).
- Your Score Report appears after you have made 6 choices.
- Your Game Score is reduced by the number of butterfly hits.
- To slow the game speed repeat tap/click on the word Slider.
- To increase the game speed repeat tap/click on the word Math.
- Speed can also be adjusted with a keyboard's - and + keys.
- Refresh/Reload the web page to restart the game.
- Adjust the sound level of media on your device.
E0